|
I am an Assistant Professor at The Zhejiang University-University of Illinois Urbana-Champaign Institute (ZJUI), Zhejiang University. I was a Project Assistant Professor at the Kabashima Lab in the Institute for Physics of Intelligence (i π), The University of Tokyo (UTokyo) from April 2022 to March 2023. I completed my Ph.D. in 2016 from Tsinghua University, supervised by Jianhua Lu. I received a B.E. from Xidian University in 2011. Previously I was a postdoctoral researcher in i π , UTokyo under supervision of Yoshiyuki Kabashima from April 2020 to March 2022, and a postdoctoral researcher in the Approximate Bayesian Inference Team, RIKEN center for Advanced Intelligence Project ( RIKEN-AIP) under supervision of Emtiyaz Khan from July 2019 to March 2020. I was a visiting researcher at University of Illinois Urbana-Champaign Institute (UIUC) from August 2023 to December 2023, hosted by Zhi-Pei Liang. I am broadly interested in the intersection of machine learning, information theory, and statistical mechanics, with a special focus on graphical models, Bayesian inference, and learning algorithms. Email / Google Scholar / Github / Blog / ZJU page / |

|
|
News: One paper was accepted by ICASSP2026.
News: I was invited to serve as an Area Chair for ICML 2026.
News: One paper was accepted by ICCV2025.
News: One paper was accepted by CVPR2025 (Highlighed Paper).
News: I was invited to serve as an Area Chair for NeurIPS 2025.
News: One paper was accepted by ICLR2025.
News: I was invited to serve as an Area Chair for ICML 2025.
News: Our DMPS paper has won ACML Best Paper Runner-UP award. News: I was invited to serve as an Area Chair for ICLR 2025.
News: One paper was accepted by IJCAI 2024.
News: I was invited to serve as an Area Chair for NeurIPS 2024.
News: Our paper QCM-SGM+: Improved Quantized Compressed Sensing With Score-Based Generative Models was accepted by AAAI 2024.
News: I am looking for postdoctoral researchers and research assistants. Please send me your detailed CV if you are interested.
News: I joined ZJUI as a tensure-track assistant professor from March 20th, 2023.
News: Our paper Quantized Compressed Sensing with Score-Based Generative Models was accepted by ICLR 2023. News: Our paper On Model Selection Consistency of Lasso for High-Dimensional Ising Models was accepted by AISTATS 2023. News: Our paper Average case analysis of Lasso under ultra sparse conditions was accepted by AISTATS 2023. News: Our paper Exact Solutions of a Deep Linear Network was accepted by NeurIPS 2022. |
|
I am always looking for highly motivated postdoctoral researchers and research assistants with a great passion for doing research in machine learning, signal processing, wireless communication, and other related fields. Please send your detailed CV (including education background, publication list, and research interests) to the email address above if you are interested. |
|
My research interests lie at the intersection of machine learning, information theory and statistical mechanics, with an exploration of common principles within different fields. Specific focuses are graphical models, Bayesian inference, and learning algorithms. For an up-to-date publication list, please see the Google Scholar page. (*correspondence) |

|
With the rapid development of diffusion models and flow-based generative models, there has been a surge of interests in solving noisy linear inverse problems, e.g., super-resolution, deblurring, denoising, colorization, etc, with generative models. However, while remarkable reconstruction performances have been achieved, their inference time is typically too slow since most of them rely on the seminal diffusion posterior sampling (DPS) framework and thus to approximate the intractable likelihood score, time-consuming gradient calculation through back-propagation is needed. To address this issue, this paper provides a fast and effective solution by proposing a simple closed-form approximation to the likelihood score. For both diffusion and flow-based models, extensive experiments are conducted on various noisy linear inverse problems such as noisy super-resolution, denoising, deblurring, and colorization. In all these tasks, our method (namely DMPS) demonstrates highly competitive or even better reconstruction performances while being significantly faster than all the baseline methods. |

|
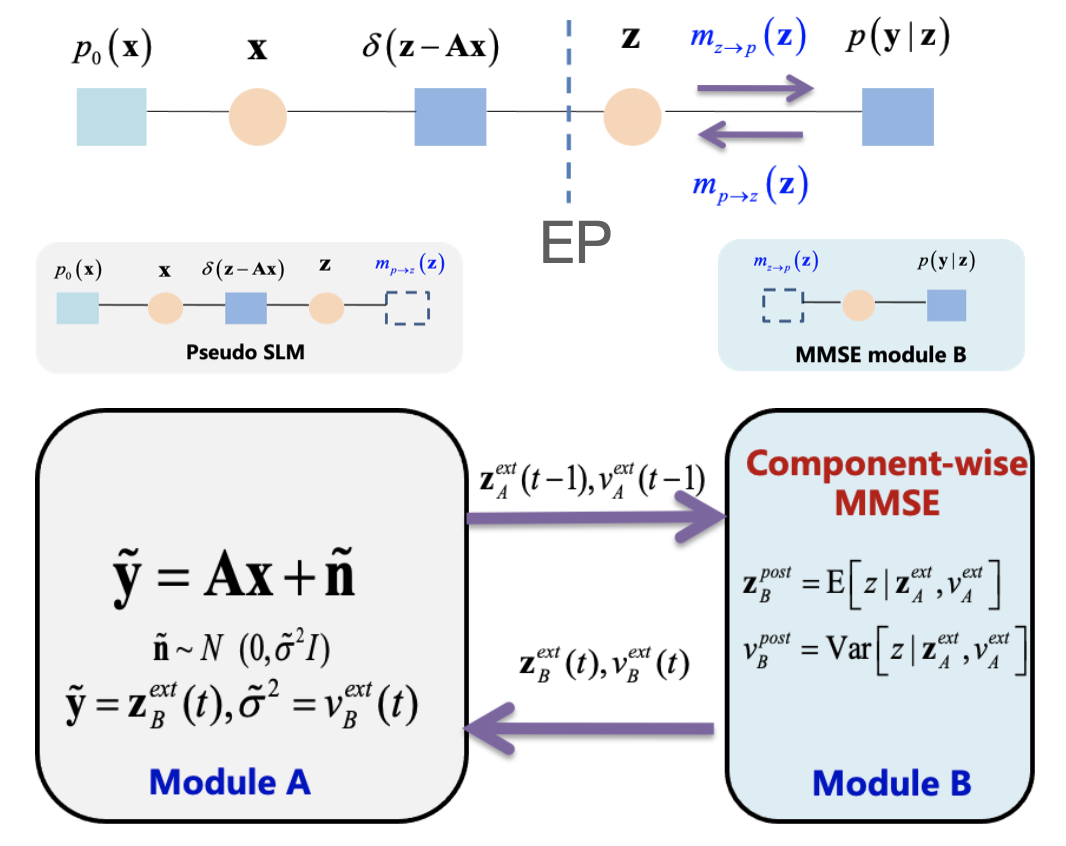
In practical compressed sensing (CS), the obtained measurements typically necessitate quantization to a limited number of bits prior to transmission or storage. This nonlinear quantization process poses significant recovery challenges, particularly with extreme coarse quantization such as 1-bit. Recently, an efficient algorithm called QCS-SGM was proposed for quantized CS (QCS) which utilizes score-based generative models (SGM) as an implicit prior. Due to the adeptness of SGM in capturing the intricate structures of natural signals, QCS-SGM substantially outperforms previous QCS methods. However, QCS-SGM is constrained to (approximately) row-orthogonal sensing matrices as the computation of the likelihood score becomes intractable otherwise. To address this limitation, we introduce an advanced variant of QCS-SGM, termed QCS-SGM+, capable of handling general matrices effectively. The key idea is a Bayesian inference perspective on the likelihood score computation, wherein an expectation propagation algorithm is employed for its approximate computation. We conduct extensive experiments on various settings, demonstrating the substantial superiority of QCS-SGM+ over QCS-SGM for general sensing matrices beyond mere row-orthogonality. |

|
We consider the general problem of recovering a high-dimensional signal from noisy quantized measurements. Quantization, especially coarse quantization such as 1-bit sign measurements, leads to severe information loss and thus a good prior knowledge of the unknown signal is helpful for accurate recovery. Motivated by the power of score-based generative models (SGM, also known as diffusion models) in capturing the rich structure of natural signals beyond simple sparsity, we propose an unsupervised data-driven approach called quantized compressed sensing with SGM (QCS-SGM), where the prior distribution is modeled by a pre-trained SGM. To perform posterior sampling, an annealed pseudo-likelihood score called noise perturbed pseudo-likelihood score is introduced and combined with the prior score of SGM. The proposed QCS-SGM applies to an arbitrary number of quantization bits. Experiments on a variety of baseline datasets demonstrate that the proposed QCS-SGM significantly outperforms existing state-of-the-art algorithms by a large margin for both in-distribution and out-of-distribution samples. Moreover, as a posterior sampling method, QCS-SGM can be easily used to obtain confidence intervals or uncertainty estimates of the reconstructed results. |
|
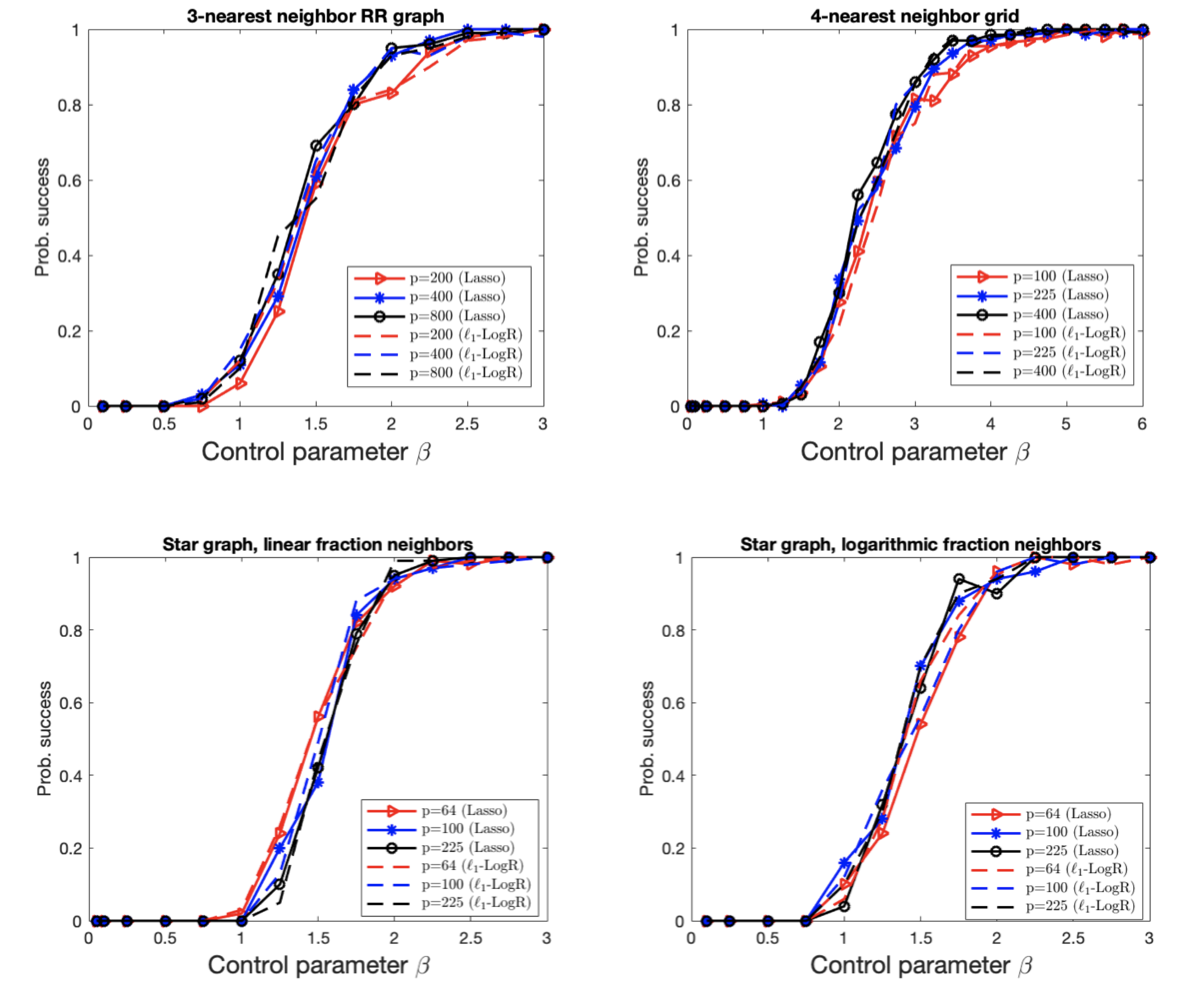
We theoretically analyze the model selection consistency of least absolute shrinkage and selection operator (Lasso) for high-dimensional Ising models. For general tree-like graphs, it is rigorously proved that Lasso without post-thresholding is model selection consistent in the whole paramagnetic phase with the same order of sample complexity as that of L1-regularized logistic regression (L1-LogR). This result is consistent with the conjecture in Meng, Obuchi, and Kabashima 2021 using the non-rigorous replica method from statistical physics and thus complements it with a rigorous proof. Moreover, we provide a rigorous proof of the model selection consistency of Lasso with post-thresholding for general tree-like graphs in the paramagnetic phase without further assumptions on the dependency and incoherence conditions. |
|
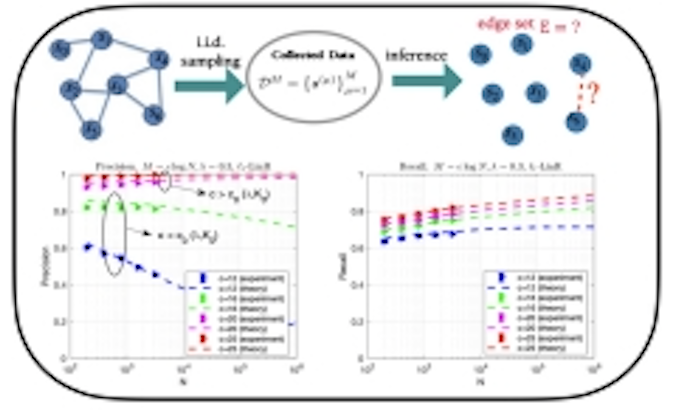
We theoretically investigate the typical learning performance of L1-regularized linear regression (L1-LinR, i.e., Lasso) for Ising model selection using the replica method from statistical mechanics. We obtain an accurate estimate of the typical sample complexity of L1-LinR, which demonstrates that L1-LinR is model selection consistent with M=0(log N) samples, where N is the number of variables of the Ising model. Moreover, we provide a computationally efficient method to accurately predict the non-asymptotic behavior of L1-LinR for moderate M and N, such as the precision and recall rates. |
|
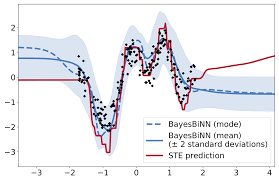
Neural networks with binary weights are computation-efficient and hardware-friendly, but their training is challenging because it involves a discrete optimization problem. Surprisingly, ignoring the discrete nature of the problem and using gradient-based methods, such as Straight-Through Estimator, still works well in practice. This raises the question: are there principled approaches which justify such methods? In this paper, we propose such an approach using the Bayesian learning rule. The rule, when applied to estimate a Bernoulli distribution over the binary weights, results in an algorithm which justifies some of the algorithmic choices made by the previous approaches. The algorithm not only obtains state-of-the-art performance, but also enables uncertainty estimation and continual learning to avoid catastrophic forgetting. Our work provides a principled approach for training binary neural networks which also justifies and extends existing approaches. |
|
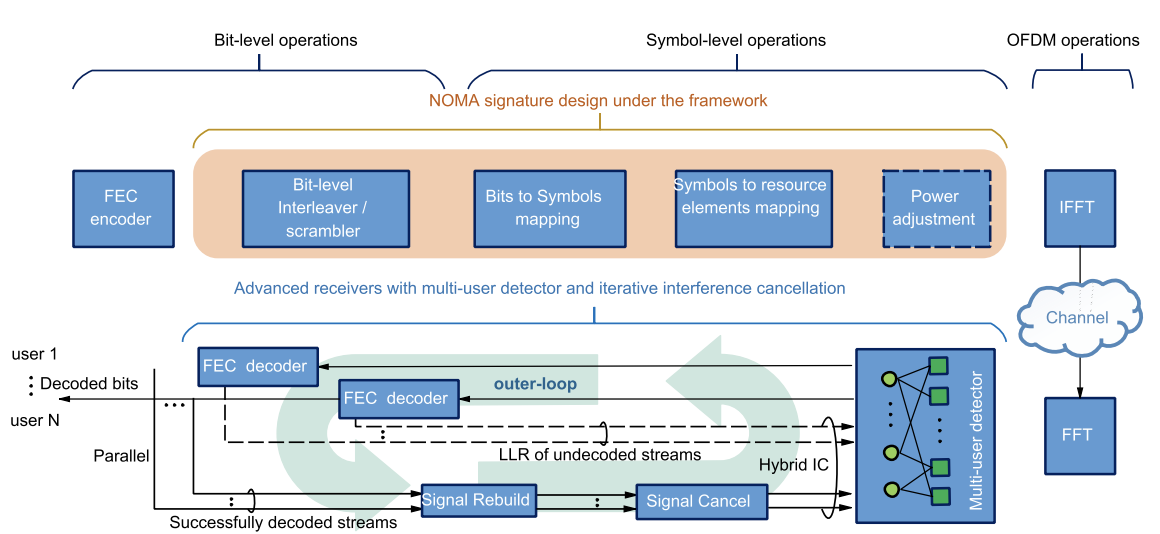
Our proposed EPA receiver has been officially written into 3GPP TR38.812, adopted as one of the three main receivers for NOMA enabled 5G base stations. Non-orthogonal multiple access (NOMA) on shared resources has been identified as a promising technology in 5G to improve resource efficiency and support massive access in all kinds of transmission modes. Power domain and code domain NOMA have been extensively studied and evaluated in both literatures and 3GPP standardization, especially for the uplink where large number of users would like to send their messages to the base station. Though different in the transmitter side design, power domain NOMA and code domain NOMA share the same need of the advanced multi-user detection (MUD) design at the receiver side. Various multi-user detection algorithms have been proposed, balancing performance and complexity in different ways, which is important for the implementation of NOMA in practical networks. In this paper, we introduce a unified variational inference (VI) perspective on various universal NOMA MUD algorithms such as belief propagation (BP), expectation propagation (EP), vector EP (VEP), approximate message passing (AMP) and vector AMP (VAMP), demonstrating how they could be derived from and adapted to each other within the VI framework. Moreover, we unveil and prove that conventional elementary signal estimator (ESE) and linear minimum mean square error (LMMSE) receivers are special cases of EP and VEP, respectively, thus bridging the gap between classic linear receivers and message passing based nonlinear receivers. Such a unified perspective would not only help the design and adaptation of NOMA receivers, but also open a door for the systematic design of joint active user detection and multi-user decoding for sporadic grant-free transmission. |
|
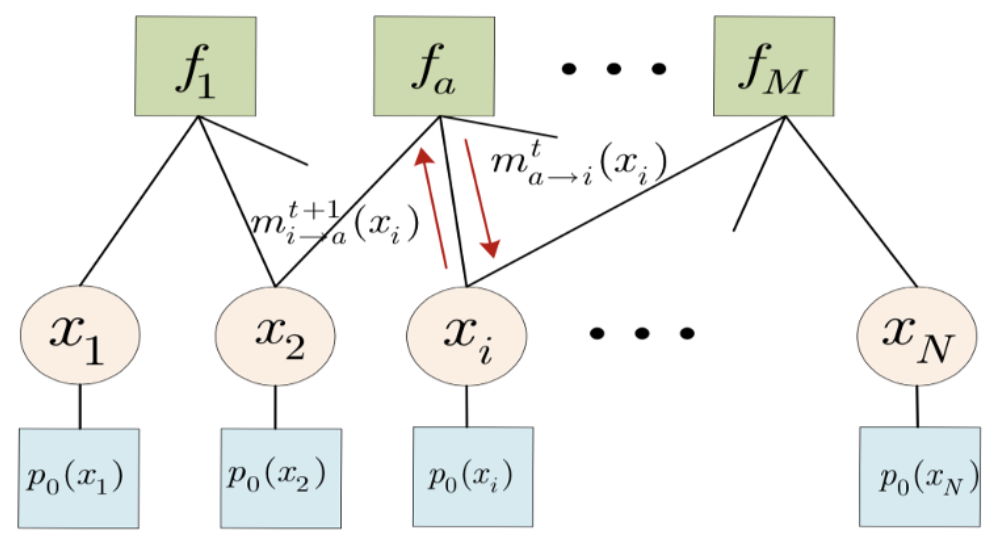
Based on expectation propagation (EP), we present a unified Bayesian inference framework for generalized linear models (GLM) which iteratively reduces the GLM problem to a sequence of standard linear model (SLM) problems. This framework provides new perspectives on some existing GLM algorithms and also suggests novel extensions for some other SLM algorithms. Specific instances elucidated under such framework are the GLM versions of approximate message passing (AMP), vector AMP (VAMP), and sparse Bayesian learning (SBL). In particular, we provide an EP perspective on the famous generalized approximate message passing (GAMP) algorithm, which leads to a concise derivation of GAMP via EP. |
|
An alternative derivation for the well-known approximate message passing (AMP) algorithm proposed by Donoho is presented in this letter. Compared with the original derivation, which exploits central limit theorem and Taylor expansion to simplify belief propagation (BP), our derivation resorts to expectation propagation (EP) and the neglect of high-order terms in large system limit. This alternative derivation leads to a different yet provably equivalent form of message passing, which explicitly establishes the intrinsic connection between AMP and EP, thereby offering some new insights in the understanding and improvement of AMP. |
|
|
|
|
|
|
|
|
|
|
|
|
I love reading, music, and table tennis. |
|
Based on this website and this website. |